Cats is a library which provides abstractions for functional programming in the Scala programming language. The name is a playful shortening of the word category.
Recursive functions are very common in functional programming. The concept is for a function to call itself until it reaches a state simple enough to solve.
To show the value of recursive methods, the Fibonacci problem is often used.
def fib(n: Int): Int = n match {
case 0 => 0
case 1 => 1
case n => fib(n-1) + fib(n-2)
}
The method will call itself over and over again until it reaches 0 or 1. The recursion makes the logic quite obvious compared to a solution with a mutable state and a loop.
The fib function has a few questionable decisions; e.g. negative numbers, Int type. To avoid focusing on the wrong problems, the rest of the article will focus on the following function.
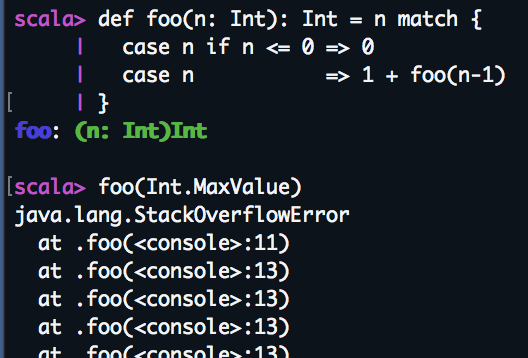
def foo(n: Int): Int = n match {
case n if n <= 0 => 0
case n => 1 + foo(n-1)
}
foo counts the positive numbers between 0 and n. The function is over-engineered but highlights a common issue with recursive functions.
Function invocations create a new stack frame. The memory holds the function’s parameters and local variables. When the application reaches the end of the function, it releases the memory.
The foo function will create n stack frames before releasing them all. If n is big enough, the application will run out of stack memory and throw a stack overflow error.
To overcome this, some languages, like Scala, offer tail recursion. It allows recursive calls to reuse the parent stack frame instead of creating a child. This removes the risk of stack overflows. For the compiler to optimize the function, it must end with the recursive call.
foo’s last operation is currently an addition. Updates are required.
def foo(n: Int): Int = {
@annotation.tailrec
def rec(n: Int, acc: Int): Int = n match {
case n if n <= 0 => acc
case n => rec(n - 1, acc + 1)
}
rec(n, 0)
}
This tail-recursive foo can run for any n without throwing any errors. While it is safer, it doesn’t solve all recursion issues. The compiler is unable to optimize alternating calls between many recursive functions. Each call will create a stack frame and eventually throw a stack overflow error.
def foo(n: Int, acc: Int): Int = n match {
case n if n <= 0 => acc
case n => bar(n - 1, acc + 1)
}
def bar(n: Int, acc: Int): Int = n match {
case n if n <= 0 => acc
case n => foo(n - 1, acc + 1)
}
A way of overcoming the issue is with trampolines. A tail-recursive function receives as argument a result or a request. The result is the instant solution, like the 0 and 1 from the Fibonacci solution. On the other hand, the request will return a result or another request.
sealed trait Trampoline[T]
case class Result[T](value: T) extends Trampoline[T]
case class Request[T](f: () => Trampoline[T]) extends Trampoline[T]
@annotation.tailrec
def run[T](trampoline: Trampoline[T]): T = trampoline match {
case Result(value) => value
case Request(f) => run(f())
}
def foo(n: Int): Int = run(Request(() => foo(n, 0)))
def foo(n: Int, acc: Int): Trampoline[Int] = n match {
case n if n <= 0 => Result(acc)
case n => Request(() => bar(n - 1, acc + 1))
}
def bar(n: Int): Int = run(Request(() => bar(n, 0)))
def bar(n: Int, acc: Int): Trampoline[Int] = n match {
case n if n <= 0 => Result(acc)
case n => Request(() => foo(n - 1, acc + 1))
}
Cats Eval is yet another solution. It comes with three constructs to represent eager, lazy, and memoized evaluation. Furthermore, it implements map and flatMap. This makes the following function more readable than the previous trampoline and tail-recursive ones.
import cats._
def foo(n: Int): Eval[Int] = n match {
case n if n <= 0 => Eval.now(0)
case n => Eval.defer(foo(n - 1).map(_ + 1))
}
def bar(n: Int): Eval[Int] = n match {
case n if n <= 0 => Eval.now(0)
case n => Eval.defer(foo(n - 1).map(_ + 1))
}
If you are struggling to write a tail recursion function, or you just prefer more readable code, have a look at Eval. It won’t revolutionize your code, but will definitely make it more stable.